Kernel regression
- Not to be confused with Kernel principal component analysis.
The kernel regression is a non-parametric technique in statistics to estimate the conditional expectation of a random variable. The objective is to find a non-linear relation between a pair of random variables X and Y.
In any nonparametric regression, the conditional expectation of a variable  relative to a variable
relative to a variable  may be written:
may be written:
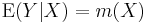
where  is an unknown function.
is an unknown function.
Contents |
Nadaraya-Watson kernel regression
Nadaraya (1964) and Watson (1964) proposed to estimate  as a locally weighted average, using a kernel as a weighting function. The Nadaraya-Watson estimator is:
as a locally weighted average, using a kernel as a weighting function. The Nadaraya-Watson estimator is:
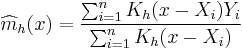
where  is a kernel with a bandwidth
is a kernel with a bandwidth  . The fraction is a weighting term with sum 1.
. The fraction is a weighting term with sum 1.
Derivation
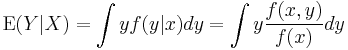
Using the kernel density estimation for the joint distribution f(x,y) and f(x) with a kernel K,
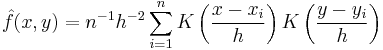 ,
,
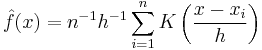
we obtain the Nadaraya-Watson estimator.
Priestley-Chao kernel estimator
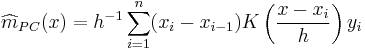
Gasser-Müller kernel estimator
![\widehat{m}_{GM}(x) = h^{-1} \sum_{i=1}^n \left[\int_{s_{i-1}}^{s_i} K\left(\frac{x-u}{h}\right) du\right] y_i](/2012-wikipedia_en_all_nopic_01_2012/I/9efb47c3c8770b0b974512e124a80a28.png)
where 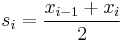
Example
This example is based upon Canadian cross-section wage data consisting of a random sample taken from the 1971 Canadian Census Public Use Tapes for male individuals having common education (grade 13). There are 205 observations in total.
We consider estimating the unknown regression function using Nadaraya-Watson kernel regression via the R np package that uses automatic (data-driven) bandwidth selection; see the np vignette for an introduction to the np package.
The figure below shows the estimated regression function using a second order Gaussian kernel along with asymptotic variability bounds
Script for example
The following commands of the R programming language use the npreg() function to deliver optimal smoothing and to create the figure given above. These commands can be entered at the command prompt via cut and paste.
library(np) /* non parametic library */
data(cps71)
attach(cps71)
m <- npreg(logwage~age)
plot(m,plot.errors.method="asymptotic",
plot.errors.style="band",
ylim=c(11,15.2))
points(age,logwage,cex=.25)
Related
According to Salsburg(2002, page 290-291), the algorithms used in kernel regression were independently developed and used in Fuzzy Systems: "Coming up with almost exactly the same computer algorithm, fuzzy systems and kernel density-based regressions appear to have been developed completely independently of one another."
References
- Nadaraya, E. A. (1964). "On Estimating Regression". Theory of Probability and its Applications 9 (1): 141–142. doi:10.1137/1109020.
- Li, Qi; Racine, Jeffrey S. (2007). Nonparametric Econometrics: Theory and Practice. Princeton University Press. ISBN 0691121613.
- Simonoff, Jeffrey S. (1996). Smoothing Methods in Statistics. Springer. ISBN 0-387-94716-7.
- Salsburg, D. (2002) The Lady Tasting Tea: How Statistics Revolutionized Science in the Twentieth Century, W.H. Freeman / Owl Book. ISBN 0-8050-7134-2
- C. Richard, J. C. M. Bermudez, and P. Honeine. "Online prediction of time series data with kernels," IEEE Transactions on Signal Processing, 57(3):1058-1066, 2009.
Statistical implementation
kernreg2 y x, bwidth(.5) kercode(3) npoint(500) gen(kernelprediction gridofpoints)
- R: npreg (package np)
- GNU/octave mathematical program package:
External links
- Scale-adaptive kernel regression (with Matlab software).
- An online kernel regression demonstration Requires .NET 3.0 or later.
- The np package An R package that provides a variety of nonparametric and semiparametric kernel methods that seamlessly handle a mix of continuous, unordered, and ordered factor data types.